ENTUAL Chessbot Part 2
Schach, das königliche Spiel, ist eines der ältesten Brettspiele der Welt. Seit Jahrhunderten messen sich Begeisterte des Schachsports in ihrem strategischen Denken und bewegen hochkonzentriert die 32 Figuren vor sich hin, die Entual Kollegen sind da natürlich auch keine Ausnahme.
Während in der prä-digitalisierten Ära Spieler wie Bobby Fischer und Boris Spassky das Geschehen am Brett dominierten, sind es heute KI-gesteuerte Schachprogramme, die nicht zu bezwingen sind. Selbst aktuelle Großmeister wie Magnus Carlsen oder Hikaru Nakamura müssen sich dem Einsatz moderner Technik schon lange geschlagen geben.
Das prominenteste und derzeit stärkste Schachprogramm ist Stockfish, das sich unter anderem neuronaler Netze bedient, um die stärksten Züge in jeder Position zu finden.
Doch wie funktioniert eigentlich ein solcher Schachcomputer? Welche Algorithmen kommen zum Einsatz, um sogar die stärksten menschlichen Spieler in die Knie zu zwingen? Kann man einen Schachcomputer so ohne weiteres selber programmieren?
Entual hat sich im Sommer mit diesen Fragen beschäftigt. Herausgekommen ist dabei ein Prototyp eines Schachcomputers, powered by Ab Initio, mit dem auch einigermaßen fortgeschrittene Spieler ihre Probleme haben werden.
Im vorherigen Blogpost haben wir uns ausführlich der FEN-Notation und der grundlegenden Funktionalität eines Schachcomputers gewidmet. Nun wenden wir uns der Ermittlung aller möglichen Züge einer bestimmten Brettstellung zu und beleuchten, wie eine Bewertungsfunktion der jeweiligen Züge umgesetzt werden kann.

https://www.pexels.com/photo/man-holding-chess-piece-277124/
Zugermittlung
Bevor der Schachcomputer den besten Zug einer bestimmten Brettstellung angeben kann, muss er zunächst sämtliche mögliche Züge ermitteln. Dafür wird über alle noch existierenden Figuren des gerade zugberechtigten Spielers iteriert. Unter Berücksichtigung der Position, auf der sich die Figur befindet und unter Anwendung der bekannten Regeln wie die einzelnen Figuren ziehen können, werden nun die legalen Züge eines Spielers ermittelt. Dabei muss besonders darauf geachtet werden, dass Züge, die ein Schachgebot für den eigenen König zur Folge haben, ausgeschlossen werden. Sämtliche so ermittelten Züge transformieren den FEN der Brettstellung in einen neuen FEN.
Wir analysieren den Algorithmus zur Ermittlung der Züge eines Springers exemplarisch anhand folgender Brettstellung:
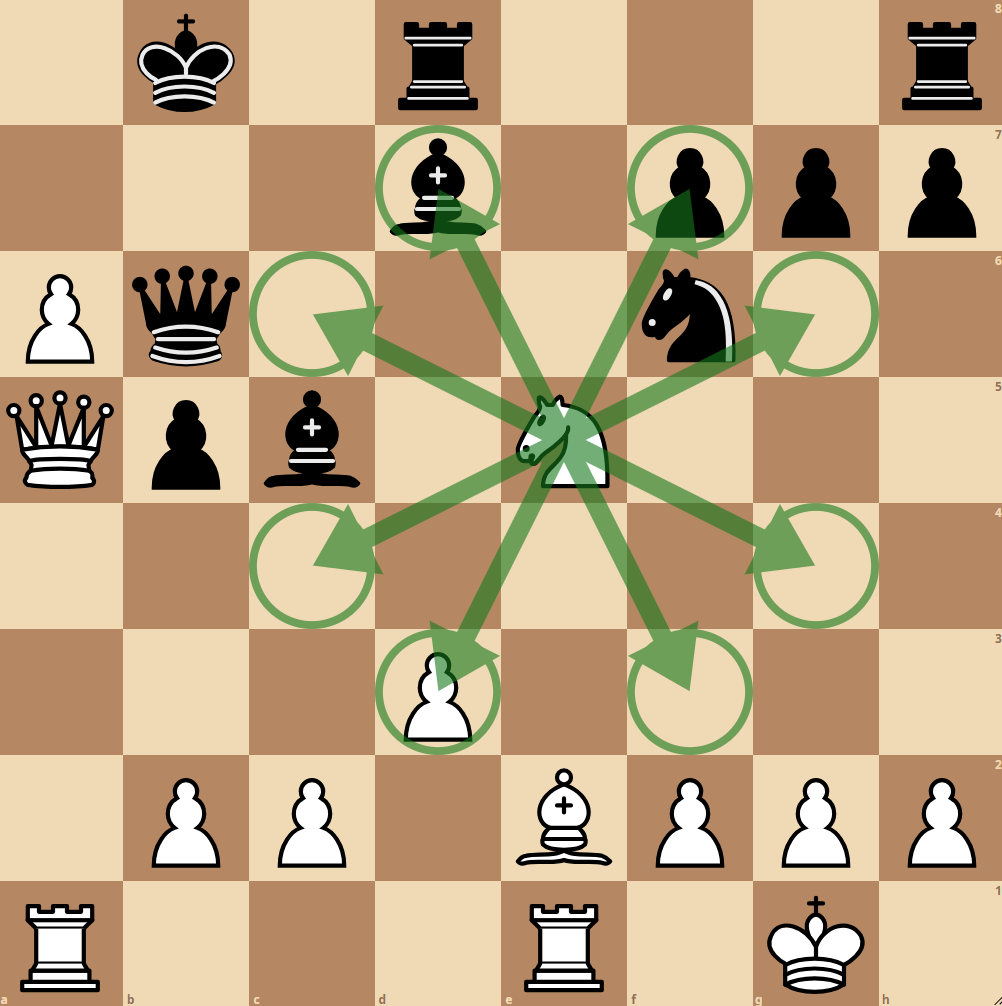
Es befinden sich acht Felder auf dem Spielbrett, die der Springer auf e5 aktuell ansteuern könnte. Legale Züge sind nun jene Züge, die im Schlagen einer gegnerischen Figur resultieren (d7 und f7) oder im Besetzen eines freien Feldes enden. Der Zug des Springers auf das Feld d3 ist hingegen ausgeschlossen, da sich dort eine Figur der eigenen Farbe befindet.
Keiner der sieben möglichen Züge resultiert in einem Schachgebot für den weißen König, weshalb sie alle valide sind.
Für Läufer, Turm und Dame funktioniert der Algorithmus zur Zugermittlung etwas anders, da keine feste Anzahl an Zielfeldern abgesucht wird. Es werden hingegen für jede der vier Bewegungsrichtungen so lange Züge ausgeführt, bis der Spielbrettrand erreicht ist, ein Schlagzug erfolgt ist oder eine Figur der eigenen Farbe im Weg steht.
Im Pseudocode sieht das dann so aus:
for each Bewegungsrichtung:
while (AUF_SPIELBRETT):
Bewege Figur ein Feld voran
if (FELD_FREI):
Neuer Zug gefunden
else if (GEGNERISCHE_FIGUR_AUF_FELD):
Neuer Zug gefunden
exit while
else if (TEAM_FIGUR_AUF_FELD or SPIELBRETT_VERLASSEN):
exit while
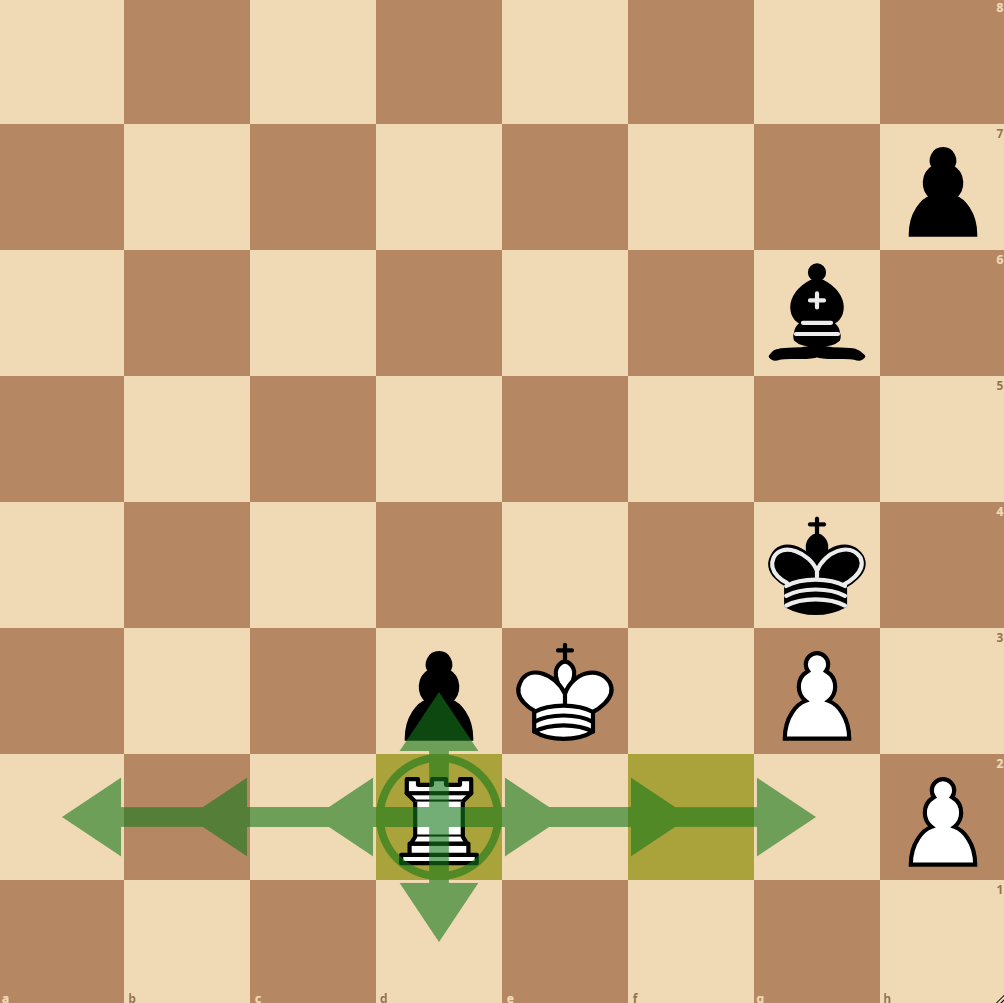
In der folgenden Darstellung werden, basierend auf dem obigen Pseudocode, die Züge eines Turms im Endspiel ermittelt, wobei die Pfeilspitzen jeweils mögliche Endpositionen symbolisieren:
Bewertungsfunktion
Im nächsten Schritt muss der Schachcomputer bewerten, welche der eben ermittelten Züge besonders vorteilhaft sind, sowie welche besser nicht gespielt werden sollten. Dafür benötigt man eine quantitative Bewertungsfunktion, die jeder Brettposition eine Zahl zuordnet. Eine positive Zahl bedeutet einen Vorteil für Weiß, eine negative Zahl einen Vorteil für Schwarz. Je höher der absolute Wert der Zahl ist, desto höher der Vorteil in der untersuchten Stellung.
Die Herausforderung des Entwicklerteams besteht nun darin, sich eine besonders sinnvolle Bewertungsfunktion einfallen zu lassen, die alle relevanten Parameter der Brettstellung berücksichtigt. Einen guten Startpunkt hierfür liefert das verbliebene Spielmaterial. Dabei werden ausgehend vom neutralen Wert 0 die Wertigkeiten der weißen Figuren addiert, sowie die der schwarzen Figuren subtrahiert. Eine allgemein akzeptierte Wertigkeit der Figuren lautet wie folgt: Dame: 9, Turm: 5, Springer: 3, Läufer: 3, Bauer: 1. Andere Faktoren, wie zum Beispiel den Entwicklungsgrad der Figuren eines Spielers oder die Königssicherheit sollten in der Bewertungsfunktion auch berücksichtigt werden. Ein zentraler Springer hat etwa eine höhere Wertigkeit als ein Randspringer. Ein weit vorangeschrittener Freibauer im Endspiel ist ebenfalls mehr Wert als ein Bauer auf seinem Startfeld.
Für die folgende Brettstellung wird nun die Bewertungsfunktion evaluiert:
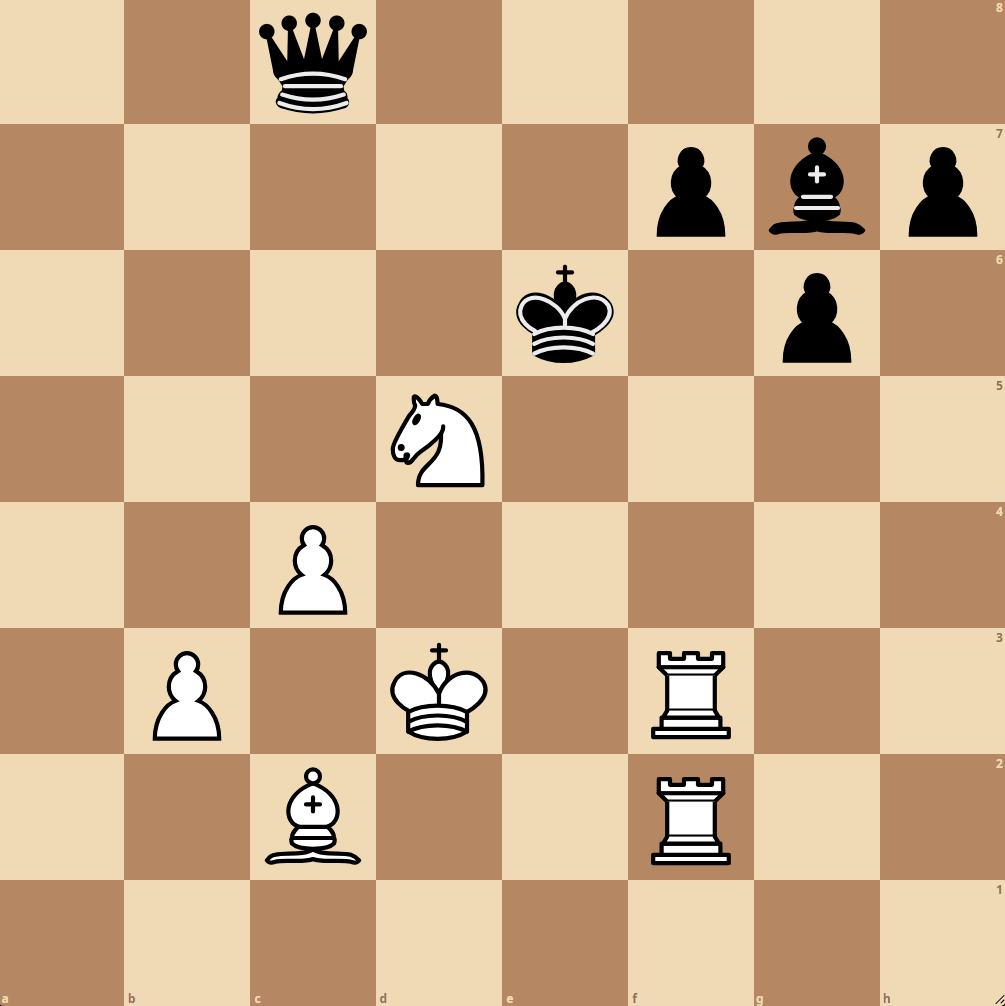
Weiß: 2 Türme (10) + 1 Springer (3) + 1 Läufer (3) + 2 Bauern (2) = 18
Schwarz: 1 Dame (9) + 1 Läufer (3) + 3 Bauern (3) = 15
Insgesamt ergibt sich dadurch ein Wert von 18-15 = +3, was einen Vorteil für den weißen Spieler bedeutet.
Aus Gründen der Einfachheit werden wir im weiteren Verlauf von einer Bewertungsfunktion ausgehen, die ausschließlich das noch am Brett befindliche Material berücksichtigt, die jedoch alle strategischen Prinzipien zunächst außer Acht lässt.
Minimax-Algorithmus
Ein rudimentärer Schachcomputer kann nun nach folgendem Prinzip gebaut werden: Für eine beliebige Brettstellung werden alle möglichen Züge ermittelt, ausgeführt und die daraus resultierende Brettstellung bewertet. Der Zug, der für Weiß zur höchsten (für Schwarz niedrigsten) Bewertung führt, wird dann ausgeführt.
Man betrachte folgende Brettstellung (Weiß am Zug):
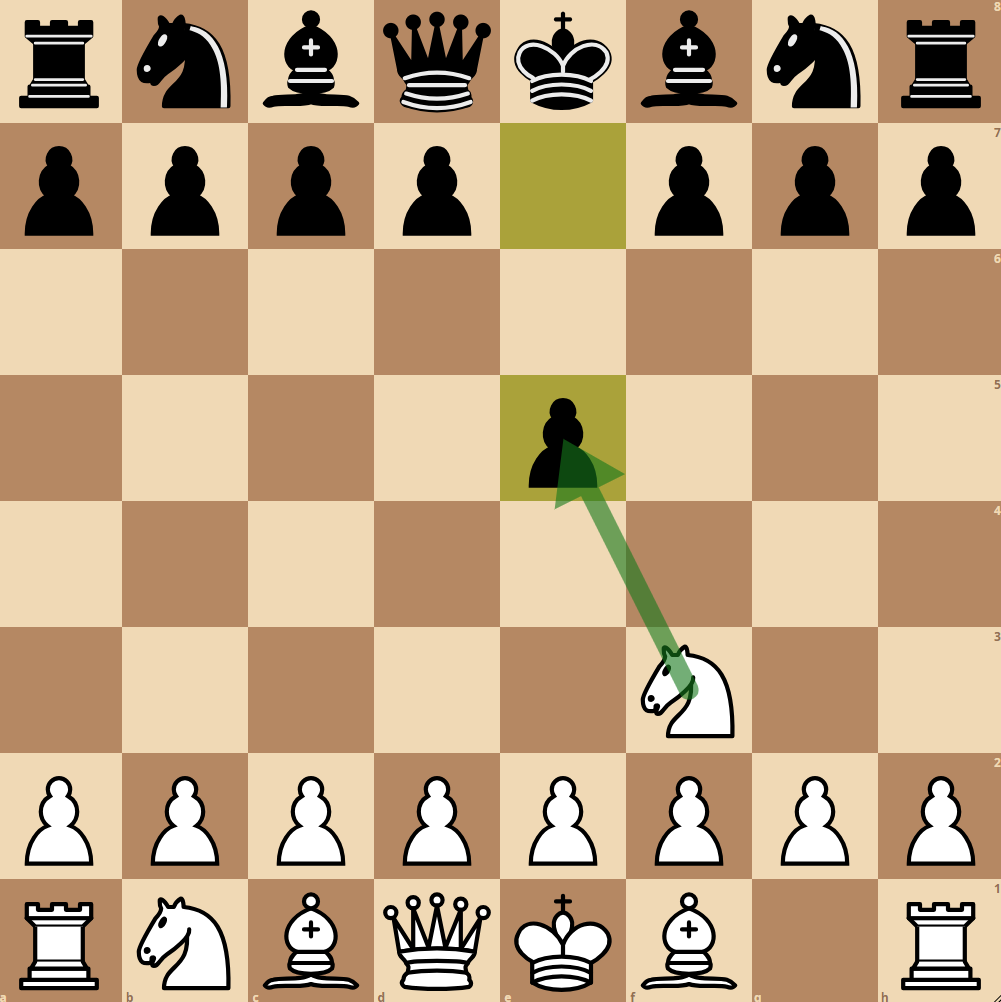
Der Zug Sxe5 führt zu einer Bewertung von +1 für Weiß, alle anderen Züge zu keinem Materialgewinn und daher zu einer ausgeglichenen Bewertung von 0. Der Schachcomputer schlägt also den Schlagzug für Weiß vor.
Man betrachte nun eine weitere Brettstellung (Weiß am Zug):
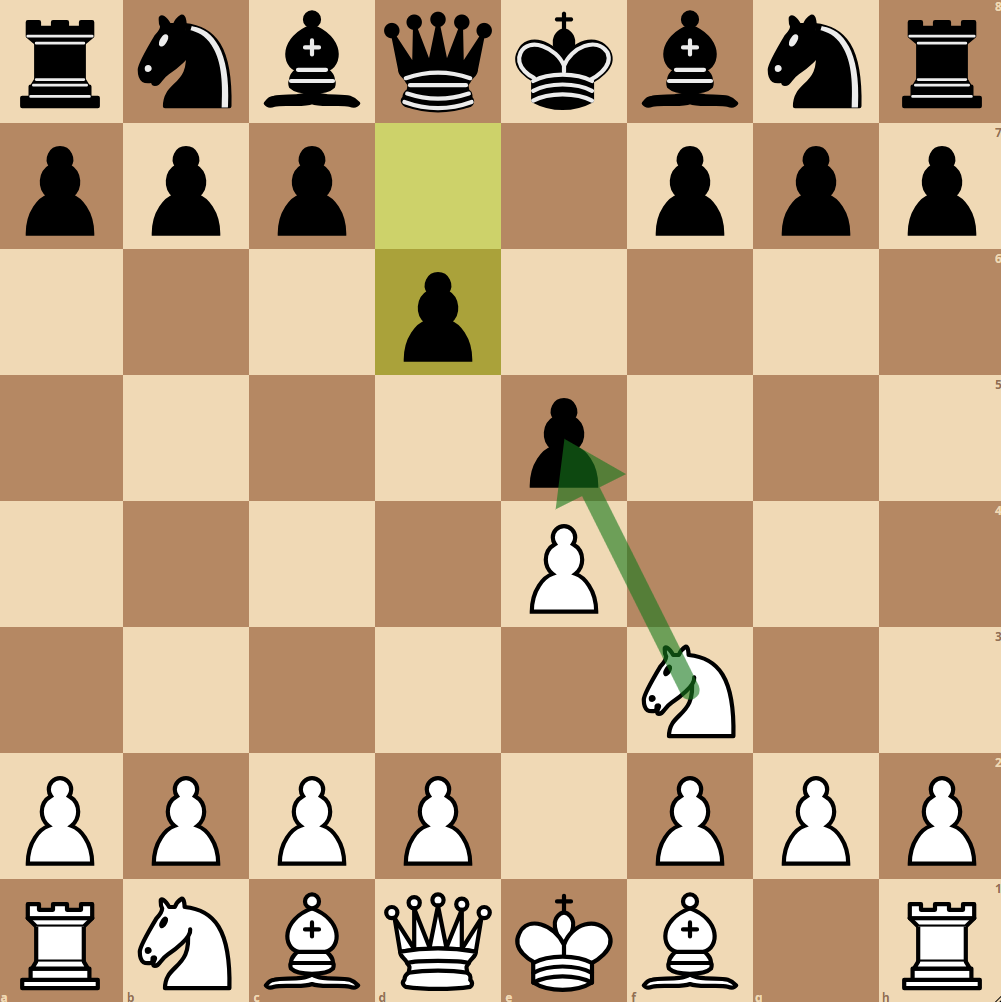
Auch hier wird der simple Schachcomputer den Schlagzug Sxe5 empfehlen, da er nach wie vor der einzige Zug ist, der zu Materialgewinn führt.
Jedem Amateurspieler ist aber natürlich sofort klar, dass der Bauer auf e5 gedeckt ist wodurch das Schlagen also kein guter Zug wäre. Der Schachcomputer muss also nicht nur alle möglichen Züge für Weiß ermitteln, sondern ebenfalls für jeden dieser Züge sämtliche schwarzen Antwortzüge. Findet sich in einem der schwarzen Antwortzüge ein unvorteilhafter Zug für Weiß, so muss der initiale weiße Zug verworfen und ein anderer Zug ausgeführt werden. Der Algorithmus muss also die Bewertungsfunktion für den weißen Spieler maximieren unter der Einschränkung, dass der schwarze Spieler versuchen wird, die Bewertungsfunktion zu minimieren. Diese Überlegung führt zum sogenannten Minimax-Algorithmus, der auch dem Entual-Chessbot zugrunde liegt.
Der Minimax-Algorithmus ist ein Algorithmus aus dem Bereich der Spieltheorie, mit dem man optimale Züge für Zwei-Personen-Spiele mit perfekter Information berechnen kann. Grundlegend für die Verwendung des Minimax-Algorithmus ist eine Bewertungsfunktion für das Spiel. Es wird davon ausgegangen, dass beide Spieler optimal spielen. Spieler Weiß versucht, die Bewertungsfunktion zu maximieren, Spieler Schwarz versucht, sie zu minimieren.
Im ersten Schritt wird ausgehend von einer Brettstellung der Spielbaum aller möglichen Züge bis in eine vordefinierte Tiefe generiert. Der Einfachheit geschuldet betrachten wir eine Tiefe von 3 und gehen davon aus, dass jeder Spieler immer nur zwei mögliche Züge zur Auswahl hat. Die Zeilen im Spielbaum repräsentieren abwechselnd den maximierenden und den minimierenden Spieler. Am untersten Ende des Spielbaums verwendet man die statische Bewertungsfunktion, um die resultierenden Brettstellungen zu quantifizieren.
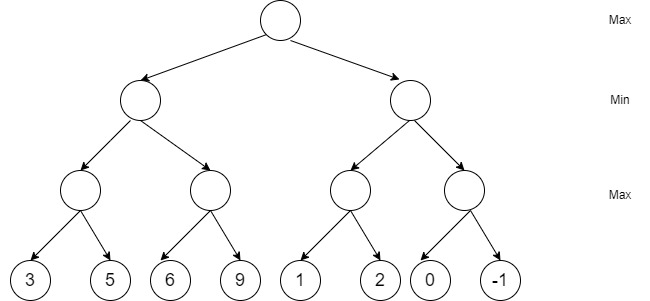
Nun wird der Spielbaum von hinten aufgerollt. Weiß ist zunächst am Zug und wählt daher immer jenen Zug aus, der die Bewertungsfunktion maximiert. Anschließend ist Schwarz am Zug und wählt daher immer jenen Zug aus, der die Bewertungsfunktion minimiert.
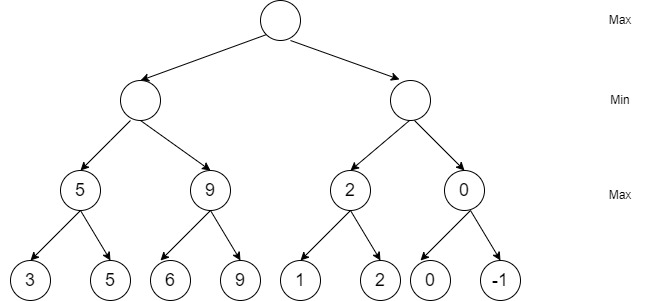
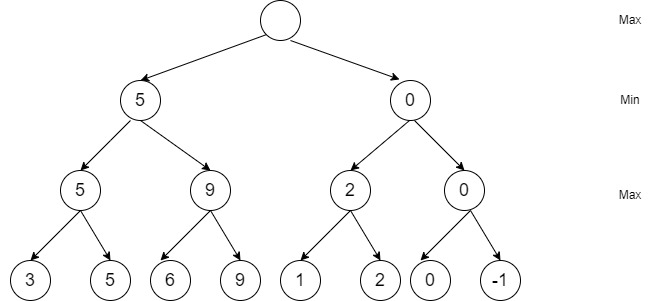
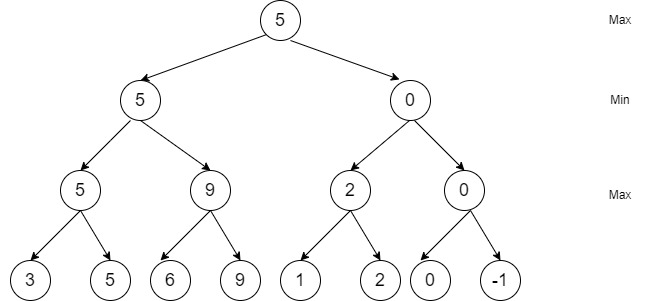
Ganz oben angekommen erhält man durch Anwendung des Minimax-Algorithmus die dynamische Stellungsbewertung der aktuellen Brettstellung sowie den besten Zug.
Ein Nachteil des Minimax-Algorithmus liegt in der schnell wachsenden Zahl der zu analysierenden Brettstellungen. Geht man von einer durchschnittlichen Anzahl von 40 möglichen Zügen pro Spieler aus, so müssten für eine Tiefe von 4 bereits 40^4 = 2560000 Stellungen analysiert werden. Des Weiteren muss in der naiven Anwendung des Algorithmus immer der gesamte Suchbaum untersucht werden, selbst für den Fall, dass gewisse Teile davon keine Auswirkungen auf das Ergebnis haben können.
Um starke taktische Stilmittel, wie etwa das temporäre Opfern einer Figur für einen erfolgreichen Angriff entdecken zu können, sind solche Tiefen jedoch unabdingbar.
Ausblick
Im nächsten Blogartikel befassen wir uns mit den technische Implementierungsthemen des Chessbots mit Ab Initio durch Continuous Graphen sowie die verwendete Ablauflogik .